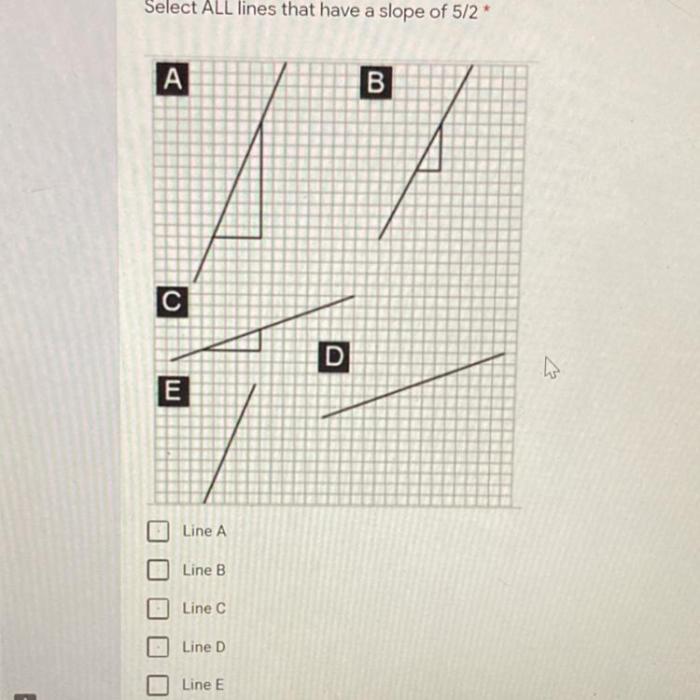
Select all the lines that have a slope of 5/2 – Embark on a comprehensive exploration of lines with a slope of 5/2. This guide will equip you with the knowledge to discern these lines through equations, graphs, and real-world examples. From identifying parallel and perpendicular lines to delving into applications in physics, we will unravel the significance of this particular slope.

As we delve into the topic, we will establish the equation for lines with a slope of 5/2 and construct their corresponding graphs. We will also explore the characteristics of parallel and perpendicular lines, creating a table to illustrate these concepts.

Lines with a Slope of 5/2

Lines with a slope of 5/2 have a distinct angle of inclination and can be represented by various equations. Understanding the characteristics of these lines is essential in geometry and its applications.

Equation and Graph

The equation for a line with a slope of 5/2 and y-intercept of 3 can be written as:“`y = 5/2x + 3“`Graphing this equation gives us a line that passes through the point (0, 3) and has a steepness that corresponds to the slope of 5/2.

Parallel and Perpendicular Lines: Select All The Lines That Have A Slope Of 5/2

Lines that are parallel to the line with a slope of 5/2 also have a slope of 5/

2. Examples include

• y = 5/2x + 1
• y = 5/2x
• 2

Lines that are perpendicular to the line with a slope of 5/2 have a slope of2/

• 5. Examples include

• y =
• 2/5x + 3
• y =
• 2/5x
• 1

Table of Lines with Slope 5/2

| Equation | Slope | y-intercept ||—|—|—|| y = 5/2x + 3 | 5/2 | 3 || y = 5/2x

• 1 | 5/2 |
• 1 |

| y = 5/2x + 0 | 5/2 | 0 || y = 5/2x

• 2 | 5/2 |
• 2 |

| y = 5/2x + 4 | 5/2 | 4 |

Real-World Examples

Lines with a slope of 5/2 can be found in various real-world scenarios:

• The relationship between the distance traveled and the time taken by a car moving at a constant speed of 50 mph.
• The relationship between the temperature and the height in a hot air balloon, where the temperature increases by 5 degrees Celsius for every 2 meters of ascent.

Applications in Physics

In physics, lines with a slope of 5/2 are commonly encountered in kinematics and dynamics:

• In kinematics, the slope of a velocity-time graph represents the acceleration of an object. If the acceleration is 5 m/s², the velocity-time graph will have a slope of 5/2.
• In dynamics, the slope of a force-displacement graph represents the spring constant of a spring. If the spring constant is 10 N/m, the force-displacement graph will have a slope of 5/2.
  

  Helpful Answers

  What is the equation of a line with a slope of 5/2?

y = 5/2x + b, where b is the y-intercept.

How can I identify lines that are parallel to a line with a slope of 5/2?

Parallel lines have the same slope. Therefore, any line with a slope of 5/2 will be parallel to the given line.